What is the geometric mean?
The geometric mean is a type of mean that is calculated as the square root of the product of a set of strictly positive numbers.
Some Important Points
- It is less sensitive to extreme values compared to the arithmetic mean.
- Cannot be used with negative numbers.
- It is useful for averaging percentages and growth rates.
Geometric Mean: Simple Explanation
Put another way, the geometric mean is a way of finding the “average” of several positive numbers, especially useful when those numbers represent growth rates or percentages. It is used by multiplying all the numbers together and then taking the square root of the total product, which gives us an average that better reflects proportional changes.
The geometric mean is particularly useful in finance for calculating the average return on investments over several periods. Its main advantage is that it provides a result that is less affected by extreme values (very high or very low) compared to the arithmetic mean.
For example, if a company had returns of 20%, 15%, 33%, and 25% in four consecutive years, the geometric mean will give us an annual average that reflects these changes more accurately than simply adding them up and dividing by four.
Geometric Mean Formula
The formula for the geometric mean is as follows:
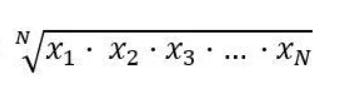
Geometric mean formula
Where:
- N: This is the total number of observations. For example, if we have the profit growth of a company over 4 periods, N will be 4.
- x: The variable X is the one on which we calculate the geometric mean. Following the previous example, the profit growth will be expressed as a percentage and will be the variable X.
- i: Represents the position of each observation. In this example, we could put a number on each period. A 1 for period 1, a 2 for period 2, etc. So x1 is the profit growth in period 1, x2 the profit growth in period 2, x3 the profit growth in period 3, and x4 the profit growth in period 4.
As we have already indicated, this type of average is suitable for calculating variables in percentages or indices. One of its main advantages is that it is less sensitive to extreme values (very large or very small) that could alter the average of a statistical sample. On the other hand, its main disadvantage is that it cannot be used with negative numbers.
Example of geometric mean
Let’s consider the results of a company. The company generated a 20% return in the first year, 15% in the second year, 33% in the third year, and 25% in the fourth year. The easy thing to do in this case would be to add up the amounts and divide by four. However, this is not correct.
To calculate the average of several percentages we must use the geometric mean. Applied to the previous case, we would have the following:

The result is 1.23, which is expressed as a percentage is 23%. This means that on average, the company has earned 23% each year. In other words, if it had earned 23% each year, it would have earned the same as earning 20% the first year, 15% the second, 33% the third, and 25% the last year.
NOTE: If the returns were negative, negative numbers would not be entered. If the return is -20%, the number to multiply would be 0.80. If the return is -5%, the number to multiply would be 0.95. In conclusion, if the returns are positive, we add the percentage in percentage to one. Whereas, if the returns or percentages are negative, we subtract the percentage in percentage to 1.
