What are vector operations?
The mathematical operations that can be applied to the coordinates of vectors are addition, subtraction, and multiplication by a scalar.
Key points
- Vector operations are essential mathematical processes that include addition, subtraction, and multiplication by a scalar.
- Vector addition is performed by adding the coordinates of each vector on the X and Y axes, resulting in a new vector.
- Vector subtraction follows a similar process, but instead of adding, the corresponding coordinates on the X and Y axes are subtracted.
- Scalar multiplication involves multiplying each coordinate of the vector by a specific number, generating a new scaled vector.
- These operations are widely used in fields such as physics, engineering, and mathematics to calculate displacements, forces, and other magnitudes that can be represented by vectors.
Vector Operations: Simple Explanation
In other words, vector operations allow us to combine and modify vectors in useful ways. They can be used to calculate displacements, forces, or any other magnitude that can be represented by vectors in space. For example, if you want to add two displacements, the vector addition operation will give you the total displacement.
Vector addition
To add two or more vectors, we will have to add the coordinates so that the axis coincides for each coordinate of the vectors. The first coordinate corresponds to the X-axis and the second coordinate corresponds to the Y-axis. Then we will have to operate on the coordinates that coincide on the axis. Schematically:
- The coordinates linked to the X axis for the following vectors are the “a” coordinate for the v vector and the “c” coordinate for the x vector.
- The coordinates linked to the Y axis for the following vectors are the “b” coordinate for the v vector and the “d” coordinate for the x vector.
The new vector will be the sum of the following vectors or it can also be defined as a new vector:
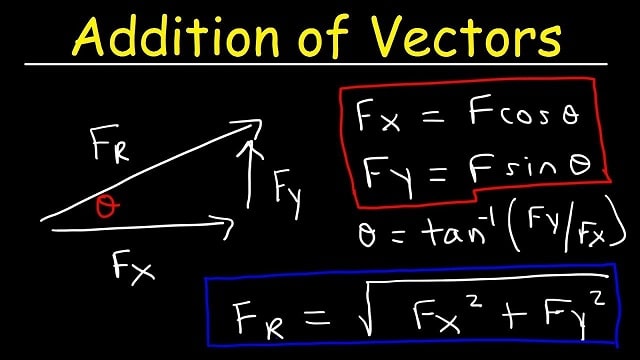
The sum of the vectors will be the sum of their coordinates respecting the axis to which they belong. We can see how the first coordinate of the sum vector is the sum of the first coordinates of the vectors (a and c). The second coordinate of the sum vector is the sum of the second coordinates of the vectors (b and d).
Vector subtraction
To subtract two or more vectors, we will have to subtract the coordinates so that the axis of each coordinate of the vectors coincides.
The first coordinate corresponds to the X-axis and the second coordinate corresponds to the Y-axis. Then we will have to operate on the coordinates that coincide on the axis. Schematically:
- The coordinates linked to the X axis for the following vectors are the “a” coordinate for the v vector and the “c” coordinate for the x vector.
- The coordinates linked to the Y axis for the following vectors are the “b” coordinate for the v vector and the “d” coordinate for the x vector.
The new vector will be the subtraction of the following vectors or it can also be defined as a new vector:
The subtraction of vectors is the subtraction of their coordinates respecting the axis to which they belong. We can see how the first coordinate of the subtraction vector is the subtraction of the first coordinates of the vectors (a and c). The second coordinate of the subtraction vector is the subtraction of the second coordinates of the vectors (b and d).
Multiplication by a scalar
The multiplication of a vector by a number (scalar) is completed by multiplying the number by the coordinates of the vector. The new vector will be the multiplication of the vector by the scalar or it can also be defined as a new vector:

